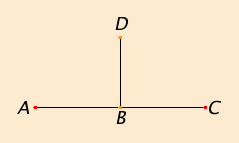Definition 10

In the figure, the two angles DBA and DBC are equal, so they are right angles by definition, and so the line BD set up on the line AC is perpendicular to it. Later there will be a postulate (Post.4) which states that all right angles are equal, and after a few propositions, it can be shown that AC is also perpendicular to BD. There are no postulates that explicitly state perpendiculars exist. Instead a construction for them is given and proved in proposition I.11. The word orthogonal is frequently used in mathematics as a synonym for perpendicular.

This is the first mention in the Elements of magnitudes being equal. There are several different kinds of magnitudes in the Elements besides angles. Lines, plane figures, and solids are also kinds of magnitudes. Some of the assumptions about magnitudes are stated later as common notions C.N., which are often called axioms. One thing that magnitudes of the same kind can be is “equal,” as the angles in this definition can be. Nowhere does Euclid explicitly state what it means for angles to be equal—or for that matter, for lines, plane figures, or solids to be equal—although much can be determined by the way he uses equality.