Proposition 14
With any straight line AB, and at the point B on it, let the two straight lines BC and BD not lying on the same side make the sum of the adjacent angles ABC and ABD equal to two right angles.
I say that BD is in a straight line with CB.
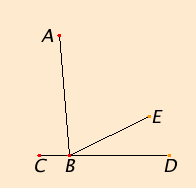
If BD is not in a straight line with BC, then produce BE in a straight line with CB.
Since the straight line AB stands on the straight line CBE, therefore the sum of the angles ABC and ABE equals two right angles. But the sum of the angles ABC and ABD also equals two right angles, therefore the sum of the angles CBA and ABE equals the sum of the angles CBA and ABD.
Subtract the angle CBA from each. Then the remaining angle ABE equals the remaining angle ABD, the less equals the greater, which is impossible. Therefore BE is not in a straight line with CB.
Similarly we can prove that neither is any other straight line except BD. Therefore CB is in a straight line with BD.
Therefore if with any straight line, and at a point on it, two straight lines not lying on the same side make the sum of the adjacent angles equal to two right angles, then the two straight lines are in a straight line with one another.