Proposition 17

In any triangle the sum of any two angles is less than two right angles.

Let ABC be a triangle.

I.17

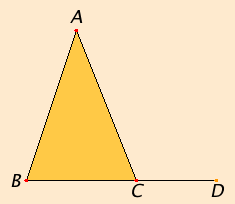
I say that the sum of any two angles of the triangle ABC is less than two right angles.

I.Post.2

Produce BC to D.

I.16
C.N.

Since the angle ACD is an exterior angle of the triangle ABC, therefore it is greater than the interior and opposite angle ABC. Add the angle ACB to each. Then the sum of the angles ACD and ACB is greater than the sum of the angles ABC and BCA.

I.13

But the sum of the angles ACD and ACB is equal to two right angles. Therefore the sum of the angles ABC and BCA is less than two right angles.

Similarly we can prove that the sum of the angles BAC and ACB is also less than two right angles, and so the sum of the angles CAB and ABC as well.

Therefore in any triangle the sum of any two angles is less than two right angles.

Q.E.D.

Guide

 The statements use the property of magnitudes This property is not listed among the Common Notions.

This proposition is strengthened in Proposition I.32 to say the sum of all three angles in a triangle equals two right angles.

Use of Proposition 17

This proposition is used in III.16 and a couple other propositions of Books III, and a few in Books VI and XI.