Proposition 2
Let A be the given point, and BC the given straight line.
It is required to place a straight line equal to the given straight line BC with one end at the point A.
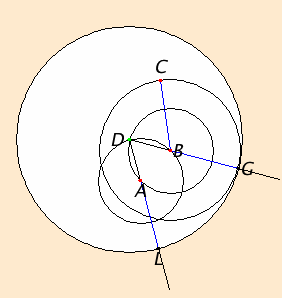
Join the straight line AB from the point A to the point B, and construct the equilateral triangle DAB on it.
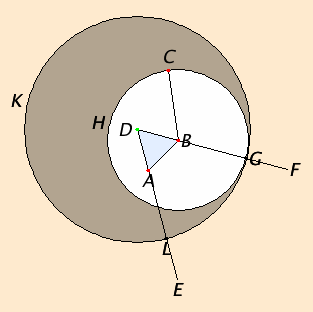
Produce the straight lines AE and BF in a straight line with DA and DB. Describe the circle CGH with center B and radius BC, and again, describe the circle GKL with center D and radius DG.
Since the point B is the center of the circle CGH, therefore BC equals BG. Again, since the point D is the center of the circle GKL, therefore DL equals DG.
And in these DA equals DB, therefore the remainder AL equals the remainder BG.
But BC was also proved equal to BG, therefore each of the straight lines AL and BC equals BG. And things which equal the same thing also equal one another, therefore AL also equals BC.
Therefore the straight line AL equal to the given straight line BC has been placed with one end at the given point A.