Proposition 22

To construct a triangle out of three straight lines which equal three given straight lines: thus it is necessary that the sum of any two of the straight lines should be greater than the remaining one.
I.20

Let the three given straight lines be A, B, and C, and let the sum of any two of these be greater than the remaining one, namely, A plus B greater than C, A plus C greater than B, and B plus C greater than B.

I.22

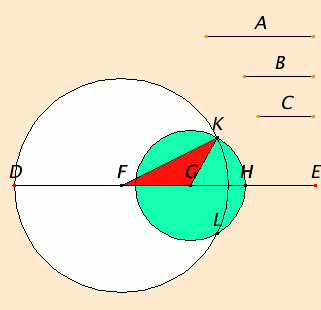
It is required to construct a triangle out of straight lines equal to A, B, and C.

I.Post.2
I.3

Set out a straight line DE, terminated at D but of infinite length in the direction of E. Make DF equal to A, FG equal to B, and GH equal to C.

I.Post.3
I.Post.1

Describe the circle DKL with center F and radius FD. Again, describe the circle KLH with center G and radius GH. Join KF and KG.

I say that the triangle KFG has been constructed out of three straight lines equal to A, B, and C.

I.Def.16
C.N.1

Since the point F is the center of the circle DKL, therefore FD equals FK. But FD equals A, therefore KF also equals A.

I.Def.16
C.N.1

Again, since the point G is the center of the circle LKH, therefore GH equals GK. But GH equals C, therefore KG also equals C.

And FG also equals B, therefore the three straight lines KF, FG, and GK equal the three straight lines A, B, and C.

Therefore out of the three straight lines KF, FG, and GK, which equal the three given straight lines A, B, and C, the triangle KFG has been constructed.

Q.E.F.

Guide

 (Be sure to change the lengths of B, C, and D in the diagram to see what effect that has. You can drag their ends to change their lengths.)

The qualifier in the statement of the proposition, “thus it is necessary that the sum of any two of the straight lines should be greater than the remaining one,” refers to the triangle inequality, Proposition I.20. This condition is, indeed, necessary. It is also sufficient, but Euclid failed to show that sufficiency. Perhaps Euclid (or some later commentator) meant this clause to be a postulate. A full statement of such a postulate might read “If the sum of the radii of two circles is greater than the line joining their centers, and if the sum of each radius and the line joining the centers is greater than the other radius, then the two circles intersect.”

This construction is actually a generalization of the very first proposition I.1 in which the three lines are all equal. There too, as was noted, Euclid failed to prove that the two circles intersected.

Use of Proposition 22

The construction in this proposition is used for the construction in proposition I.23. It is also used in XI.22