Proposition 31

To draw a straight line through a given point parallel to a given straight line.

Let A be the given point, and BC the given straight line.

I.31

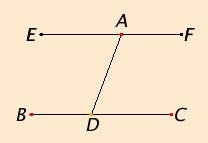
It is required to draw a straight line through the point A parallel to the straight line BC.

I.Post.1
I.23
I.Post.2

Take a point D at random on BC. Join AD. Construct the angle DAE equal to the angle ADC on the straight line DA and at the point A on it. Produce the straight line AF in a straight line with EA.

I.27

Since the straight line AD falling on the two straight lines BC and EF makes the alternate angles EAD and ADC equal to one another, therefore EAF is parallel to BC.

Therefore the straight line EAF has been drawn through the given point A parallel to the given straight line BC.

Q.E.F.

Guide

 The parallel line EF constructed in this proposition is the only one passing through the point A. If there were another, then the interior angles on one side or the other of AD it makes with BC would be less than two right angles, and therefore by the parallel postulate I.Post.5, it would meet BC, a contradiction.

Incidentally, this construction also works in hyperbolic geometry, although different parallel lines through A are constructed for different points D.

Construction steps

The construction needed is that of I.23 to construct an angle. That construction required ten circles and one line in general. In the specific case needed here, however, one of the distances does not have to be transferred, and that eliminates the need to construct four of the circles. Therefore this construction actually only requires six circles and a line.

Use of Proposition 31

This construction is frequently used in the remainder of Book I starting with the next proposition. It is also frequently used in Books II, IV, VI, XI, XII, and XIII.