Proposition 33

Straight lines which join the ends of equal and parallel straight lines in the same directions are themselves equal and parallel.

Let AB and CD be equal and parallel, and let the straight lines AC and BD join them at their ends in the same directions.

I say that AC and BD are also equal and parallel.

I.33
I.Post.1

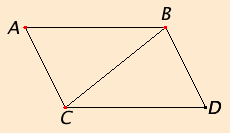
Join BC.

I.29

Since AB is parallel to CD, and BC falls upon them, therefore the alternate angles ABC and BCD equal one another.

I.4

Since AB equals CD, and BC is common, the two sides AB and BC equal the two sides DC and CB, and the angle ABC equals the angle BCD, therefore the base AC equals the base BD, the triangle ABC equals the triangle DCB, and the remaining angles equals the remaining angles respectively, namely those opposite the equal sides. Therefore the angle ACB equals the angle CBD.

I.27

Since the straight line BC falling on the two straight lines AC and BD makes the alternate angles equal to one another, therefore AC is parallel to BD.

And it was also proved equal to it.

Therefore straight lines which join the ends of equal and parallel straight lines in the same directions are themselves equal and parallel.

Q.E.D.

Guide

 The qualifier “in the same directions” in the statement of this proposition is necessary since without it the lines AD and BC could join the endpoints of the parallel lines, and AD and BC are not parallel but intersect. But these words of Euclid words are informal, and it would take some work to determine geometrically which end of AD corresponds to which end of a parallel line BC.

In general, given four points A, B, C, and D, exactly one of the three pairs of lines, AB and CD, AC and BD, and AD and BC, intersects. (If extended to infinite lines, all three pairs of lines might intersect, but as line segments only one pair does.) This statement belongs to the fundamental part of plane geometry that includes betweenness and sides of lines that wasn’t developed until the late nineteenth century.

Use of Proposition 33

This proposition is used in I.36, I.45, and a few propositions in Books XI through XIII.