Proposition 43

In any parallelogram the complements of the parallelograms about the diameter equal one another.

Let ABCD be a parallelogram, and AC its diameter, and about AC let EH and FG be parallelograms, and BK and KD the so-called complements.

I.43

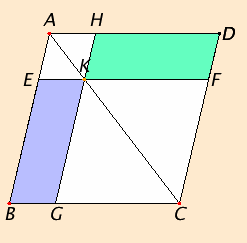
I say that the complement BK equals the complement KD.

I.34

Since ABCD is a parallelogram, and AC its diameter, therefore the triangle ABC equals the triangle ACD.

I.34

Again, since EH is a parallelogram, and AK is its diameter, therefore the triangle AEK equals the triangle AHK. For the same reason the triangle KFC also equals KGC.

C.N.2

Now, since the triangle AEK equals the triangle AHK, and KFC equals KGC, therefore the triangle AEK together with KGC equals the triangle AHK together with KFC.

C.N.3

And the whole triangle ABC also equals the whole ADC, therefore the remaining complement BK equals the remaining complement KD.

Therefore in any parallelogram the complements of the parallelograms about the diameter equal one another.

Q.E.D.

Guide

 The meaning of the statement has to be found in its use. The term “the parallelograms about the diameter” refers to the two parallelograms having the same angles as the original parallelogram and with diameters AK and KC which are two parts of a diameter AC of the original parallelogram. The complements are the two parallelograms left over after removing those two parallelograms from the original parallelogram.

Use of Proposition 43

The immediate purpose of this proposition is to change the shape of a parallelogram (one of the complements) into an equal parallelogram with the same angles (the other complement). That’s how it is used in the next proposition. It is also used in several propositions in Book II, and a couple in Book VI.