
Hypercycles, or equidistant curves are starnge curves in hyperbolic geometry that have no Euclidean counterpart.
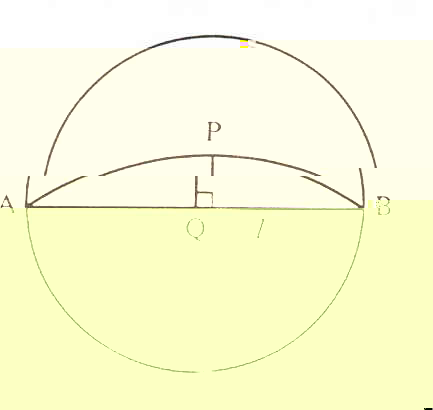
A hypercycle can be created as follows: start with a line l and a point P not on l. Consider the locus of all points on the same side of l as P and at the same pependicular distance from l as P. In Euclidean geometry this locus would just be the unique line through P parallel to l, but in hyperbolic geometry, it is not a line, it is the hypercycle through P.
In the Poincare model let A and B be the ideal end points of l. It turns out that the hypercycle to l through P is represented by the arc of the Euclidean circle passing through A,B,and P. This curve is orthogonal to all Poincare lines perpendicularto the line l.
A hypercycle is a curve traced out by a point in the hyperbolic plane that is subjected to a hyperbolic transformation. Hyperbolic transformations have two fixed points p and q, both on the unit disk. This type of transformation is called a hyperbolic translation because point move into the unit disk from one point, p or q, toward the other. The cycle traced out by this motion is a curve, where as in Euclidean geometry the same motion would create a straight line.
