Proposition 5

In isosceles triangles the angles at the base equal one another, and, if the equal straight lines are produced further, then the angles under the base equal one another.
I.Def.20
I.Post.2

Let ABC be an isosceles triangle having the side AB equal to the side AC, and let the straight lines BD and CE be produced further in a straight line with AB and AC.

I say that the angle ABC equals the angle ACB, and the angle CBD equals the angle BCE.

I.3.
I.Post.1

Take an arbitrary point F on BD. Cut off AG from AE the greater equal to AF the less, and join the straight lines FC and GB.

I.5

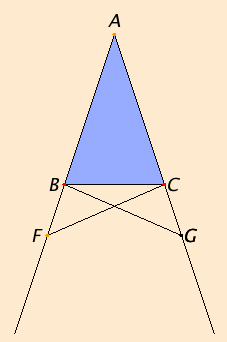
Since AF equals AG, and AB equals AC, therefore the two sides FA and AC equal the two sides GA and AB, respectively, and they contain a common angle, the angle FAG.

I.4

Therefore the base FC equals the base GB, the triangle AFC equals the triangle AGB, and the remaining angles equal the remaining angles respectively, namely those opposite the equal sides, that is, the angle ACF equals the angle ABG, and the angle AFC equals the angle AGB.

C.N.3

Since the whole AF equals the whole AG, and in these AB equals AC, therefore the remainder BF equals the remainder CG.

I.4

But FC was also proved equal to GB, therefore the two sides BF and FC equal the two sides CG and GB respectively, and the angle BFC equals the angle CGB, while the base BC is common to them. Therefore the triangle BFC also equals the triangle CGB, and the remaining angles equal the remaining angles respectively, namely those opposite the equal sides. Therefore the angle FBC equals the angle GCB, and the angle BCF equals the angle CBG.

C.N.3

Accordingly, since the whole angle ABG was proved equal to the angle ACF, and in these the angle CBG equals the angle BCF, the remaining angle ABC equals the remaining angle ACB, and they are at the base of the triangle ABC. But the angle FBC was also proved equal to the angle GCB, and they are under the base.

Therefore in isosceles triangles the angles at the base equal one another, and, if the equal straight lines are produced further, then the angles under the base equal one another.

Q.E.D.

Guide

 There are two conclusions for this proposition, first that the internal base angles ABC and ACB are equal, second that the external base angles FBC and GCB are equal. From the diagram it looks like it would be easy to prove the second conclusion from the first by simply subtracting the equal angles ABC and ACB the straight angles ABF and ACG, respectively. But Euclid doesn’t accept straight angles, and even if he did, he hasn’t proved that all straight angles are equal. Proposition I.13 would be enough, since it implies the sum of angles ABC and FBC equals two right angles, and the sum of angles ACB and GCB also equals two right angles, and so the two sums are equal effectively saying all straight angles are equal.

Unfortunately, such an argument would be circular. I.13 depends on I.11, I.11 on I.8, I.8 on I.7, and I.7 on I.5. Thus, I.13 cannot be used in the proof of I.5. It may appear that I.7 only depends on the first conclusion of I.5, but a case of I.7 that Euclid does not discuss relies on the second conclusion of I.5.

This proposition has been called the Pons Asinorum, or Asses’ Bridge. Whether this name is due to its difficulty (which it isn’t) or the resemblance of its figure to a bridge is not clear. Very few of the propositions in the Elements are known by names.

Pappus’ proof

Pappus (fl. ca. 320 C.E.) gave a much shorter proof of the first conclusion, but it is also conceptually more difficult. The two triangles BAC and CAB have two sides equal to two sides, namely side BA of the first triangle equals side CA of the second triangle, and side AC of the first triangle equal to side AB of the second, and the contained angles are equal, namely angle BAC of the first triangle equals angle CAB of the second, therefore, by I.4, the corresponding parts of the two triangles are equal, in particular, the angle B in the first triangle equals the angle C of the second.

The difficulty lies in treating one triangle as two, or in making a correspondence between a triangle and itself, but not the correspondence of identity. There is nothing wrong with this proof formally, but it might be more difficult for a student just learning geometry.

Use of Proposition 5

This proposition is used in Book I for the proofs of several propositions starting with I.7 It is also used frequently in Books II, III, IV, VI, and XIII.