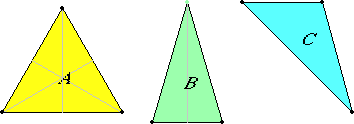
This definition classifies triangles by their symmetries, while definition 21 classifies them by the kinds of angles they contain.

The scalene triangle C has no symmetries, but the isosceles triangle B has a bilateral symmetry. The equilateral triangle A not only has three bilateral symmetries, but also has 120°-rotational symmetries.
According to this definition, an equilateral triangle is not to be considered as an isosceles triangle. The term isosceles triangle is first used in proposition I.5 and later in Books II and IV. The way that the term isosceles triangle is used in the Elements does not exclude equilateral triangles. That agrees with modern practice. It is only required that at least two sides be equal in order for a triangle to be isosceles.
Equilateral triangles are constructed in the very first proposition of the Elements, I.1. An alternate characterization of isosceles triangles, namely that their base angles are equal, is demonstrated in propositions I.5 and I.6.
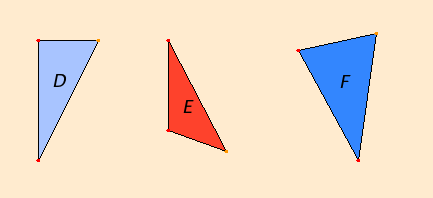
Since triangle D has a right angle, it is a right triangle. Proposition I.17 states that the sum of any two angles in a triangle is less than two right angles, therefore, no triangle can contain more than one right angle. Furthermore, there can be at most one obtuse angle, and a right angle and an obtuse angle cannot occur in the same triangle.
Triangle E is an obtuse triangle since it has an obtuse angle, while triangle F is an acute triangle since all its angles are acute.