Proposition 42
Let ABC be the given triangle, and D the given rectilinear angle.
It is required to construct in D a parallelogram equal to the triangle ABC in the rectilinear angle.
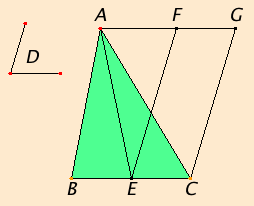
Bisect BC at E, and join AE. Construct the angle CEF on the straight line EC at the point E on it equal to the angle D. Draw AG through A parallel to EC, and draw CG through C parallel to EF.
Then FECG is a parallelogram.
Since BE equals EC, therefore the triangle ABE also equals the triangle AEC, for they are on equal bases BE and EC and in the same parallels BC and AG. Therefore the triangle ABC is double the triangle AEC.
But the parallelogram FECG is also double the triangle AEC, for it has the same base with it and is in the same parallels with it, therefore the parallelogram FECG equals the triangle ABC.
And it has the angle CEF equal to the given angle D.
Therefore the parallelogram FECG has been constructed equal to the given triangle ABC, in the angle CEF which equals D.