Proposition 10
If a straight line is bisected, and a straight line is added to it in a straight line, then the square on the whole with the added straight line and the square on the added straight line both together are double the sum of the square on the half and the square described on the straight line made up of the half and the added straight line as on one straight line.
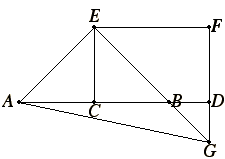
Let a straight line AB be bisected at C, and let a straight line BD be added to it in a straight line.
I say that the sum of the squares on AD and DB is double the sum of the squares on AC and CD.
Draw CE from the point C at right angles to AB and equal to either AC or CB. Join EA and EB. Draw EF through E parallel to AD, and draw FD through D parallel to CE.
Then, since a straight line EF falls on the parallel straight lines EC and FD, the sum of the angles CEF and EFD equals two right angles. Therefore the sum of the angles FEB and EFD is less than two right angles.
But straight lines produced from angles less than two right angles meet. Therefore EB and FD, if produced in the direction B and D, will meet.
Let them be produced and meet at G, and join AG.
Then, since AC equals CE, the angle EAC also equals the angle AEC. The angle at C is right, therefore each of the angles EAC and AEC is half of a right angle.
For the same reason each of the angles CEB and EBC is also half of a right angle, therefore the angle AEB is right.
And, since the angle EBC is half of a right angle, the angle DBG is also half of a right angle. But the angle BDG is also right, for it equals the angle DCE, since they are alternate. Therefore the remaining angle DGB is half of a right angle. Therefore the angle DGB equals the angle DBG, so that the side BD also equals the side GD.
Again, since the angle EGF is half of a right angle, and the angle at F is right, for it equals the opposite angle, the angle at C, the remaining angle FEG is half of a right angle. Therefore the angle EGF equals the angle FEG, so that the side GF also equals the side EF.
Now, since the square on EC equals the square on CA, the sum of the squares on EC and CA is double the square on CA. But the square on EA equals the sum of the squares on EC and CA, therefore the square on EA is double the square on AC.
Again, since FG equals EF, the square on FG also equals the square on FE. Therefore the sum of the squares on GF and FE is double the square on EF. But the square on EG equals the sum of the squares on GF and FE, therefore the square on EG is double the square on EF.
And EF equals CD, therefore the square on EG is double the square on CD. But the square on EA was also proved to be double the square on AC, therefore the sum of the squares on AE and EG is double the sum of the squares on AC and CD.
And the square on AG equals the sum of the squares on AE and EG, therefore the square on AG is double the sum of the squares on AC and CD. But the sum of the squares on AD and DG equals the square on AG, therefore the sum of the squares on AD and DG is double the sum of the squares on AC and CD.
And DG equals DB, therefore the sum of the squares on AD and DB is double the sum of the squares on AC and CD.
Therefore if a straight line is bisected, and a straight line is added to it in a straight line, then the square on the whole with the added straight line and the square on the added straight line both together are double the sum of the square on the half and the square described on the straight line made up of the half and the added straight line as on one straight line.
Q.E.D.
Guide
Outline of the proof
The proof is almost the same as the previous proposition. The entire situation is the same, except the point D is moved past the end B of the line AB.
As before draw CE at right angles to AB and equal to half of it. Finish the diagram. That results in isosceles right triangles, ACE, ECB, and EFG, as well as two other right triangles, AEG and ADG. Then,
| AG2 | = |
AE2 + EG2 |
| = |
(AC2 + CE2) +
(EF2 + FG2) |
| = |
2(AC2+CD2) |
But also,
| AG2 | = |
AD2 + DG2 |
| = |
AD2 + DB2 |
Thus, AD2 + DB2 =
2(AC2+CD2), as desired.
Interpretations of this proposition
This proposition can be interpreted to derive the same algebraic identities as the previous proposition. For example, when y is identified with CD and z is identified with CB, then the proposition states that
(y + z)2 + (y – z)2 = 2 (y2 + z2).
Side and diagonal numbers
The diagonal of a square is incommensurable with the side of a square. Another way of saying that is that the ratio of the diagonal to a side, what is generally known as the square root of 2, is not the ratio of two whole numbers, in other words √2 is an irrational number. See the Guide to proposition VIII.8 for details.
Nonetheless, finding a close rational approximation for √2 is an important goal. For practical reasons, close approximations are useful, and for theoretical reasons, close approximations are interesting.
Some time before Euclid, Plato refers in his Republic the “rational diameter” of 5. A square of side length s = 5 has a diameter (diagonal) of d = √50, which is irrational. But 49 is close to 50, so 7 is close to this irrational length. There are a number of side lengths s whose squares s2 differ from a square number d2 by only 1. The first few are displayed in the table below. The column labelled “angle” gives the angle opposite the diameter d. By the law of cosines, the cosine of the angle equals 1 – d2/(2s2).
| side s | diagonal d | relation | angle | ratio d/s |
|---|
| 1 | 1 |
2 . 12 – 1 = 12
| 60° |
1.0
|
| 2 | 3 |
2 . 22 + 1 = 32
| 97.1808° |
1.5
|
| 5 | 7 |
2 . 52 – 1 = 72
| 88.854° |
1.4
|
| 12 | 17 |
2 . 122 + 1 = 172
| 90.1989° |
1.416667
|
| 29 | 41 |
2 . 292 – 1 = 412
| 89.9659° |
1.413793
|
| 70 | 99 |
2 . 702 + 1 = 992
| 90.0058° |
1.414286
|
Note how the squares of the diagonals alternately are less and greater by 1 than twice the squares of the sides, and the angle correspondingly alternates between acute and obtuse, but quickly approaches a right angle. Likewise, the ratio d/s is alternately less and greater then the irrational number √2.
|
Note how the squares of the diagonals alternately are less and greater by 1 than twice the squares of the sides, and the angle correspondingly alternates between acute and obtuse, but quickly approaches a right angle. Likewise, the ratio d/s is alternately less and greater then the irrational number √2.
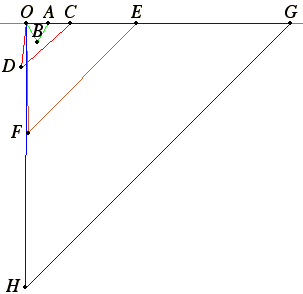
To the right are displayed triangles for the first four lines in the table. The first triangle has side
s1 = OA = 1 and diagonal
d1 = AB = 1. For the others
s2 = OC = 2 and
d2 = CD = 3;
s3 = OE = 5 and
d3 = EF = 7; also
s4 = OG = 12 and
d4 = GH = 17.
The pattern of the lengths of the sides and diagonals is evident. The next side s' is the sum of the current side and diagonal, while the next diagonal d' is the sum of twice the current side and diagonal:
s' = s + d
d' = 2s + d.
|
|
A pattern requires a verification, and this proposition supplies that. What needs to be verified is that if 2s2 differs from d2 by exactly 1, then so does
2s'2 differ from d'2 by exactly 1.
Let CD equal s, and let BC equal d. Then s' = AC = CB, and
d' = AD. By this proposition
d'2 + d2 = 2(s'2 + s2),
so that
d'2 – 2s'2 =
2s2 – d2.
Thus, if 2s2 differs from d2 by 1, then
2s'2 also differs from d'2 by 1. More precisely, if one difference is +1, then the other difference is –1.