Book I contains 23 definitions, five postulates, five common notions, and 47 propositions. Each proposition includes a proof based on the definitions, postulates, common notions, and earlier propositions. Although one could study book I sequentially, perhaps a better program is to start with the propositions and refer back to the definitions, postulates, and common notions as needed, and that is what’s done here. We’ll begin with the first proposition, I.1, and continue through the third, I.3, and refer back to the earlier material only as needed.
Proposition I.1
To construct an equilateral triangle on a given finite straight line.
The very first proposition is a construction of an equilateral triangle given one of its sides. The page for this proposition has what Euclid wrote as well as a more detailed guide for the proposition. Click here to get the page to appear in a separate window.
At the top you see the statement:
What does Euclid mean by a "construction"? His meaning is very limited.
You are allowed (1) to draw a straight line between two points and extend that line indefinitely in either direction, and (2) draw a circle given its center and a point on its circumference. A construction consists of a sequence of these two operations.
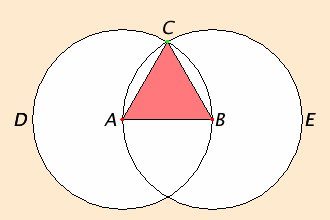
When you look at the figure and read the first few sentences, it is apparent what the construction is. You start with a line AB, draw a couple circles and a couple lines, and you're done.
There are, however, many things that need clarification before beginning. Let’s start with the concept of equilateral triangle. In his 20th definition in the book, Def.I.20, Euclid defines and equilateral triangle as a triangle with three equal sides. Note that he doesn’t include in his definition that the three angles must be equal, too; that would be called an equiangular triangle. Now, we all know that equilateral triangles are equiangular, but at this stage that has not been proved. If you skip forward to I.5, you’ll see a proposition that implies that equilateral triangles are equiangular, and the next proposition, I.6, implies that equiangular triangles are equilateral. But they come later. Here in I.1 we only need to construct a triangle with three equal sides.
The next thing to clarify is the concept of straight line. What Euclid usually meant by this is a line segment, that is, a piece of a straight line with two endpoints. His actual definition, which is found in Def.I.2 through Def.I.4, has no more useful information than the intuitive idea.
A remaining concept to clarify is that of triangle. Paraphrasing Euclid’s definition in Def.I.19, (which relies on Def.I.13 and Def.I.14) a triangle is a two-dimensional figure bounded by three straight lines as sides. There are actually a lot of subtleties in these definitions, but in a gentle introduction like this, it is best to pass over them.
Let’s return to the construction in I.1. We begin with a straight line AB which is to be one side of the constructed equilateral triangle. That is the given datum. We are then instructed to draw a circle with center A and radius AB. Over to the right of this statement is a reference to Postulate 3. This brings us to the concept of "postulate". For Euclid, a "postulate" was a statement about the particular subject of geometry that is to be assumed true. Postulates do not have proofs; they’re literally taken for granted. This particular one, Post.3, says that given a point, such as A, which is to be the center of a circle, and another point B, which is to be on the circumference of a circle, you can construct the required circle. This postulate is an assumed construction, something that says a particular thing, in this case a circle, exists. So Post.3 is the justification required for the first construction in I.1. Every statement in a proof requires some kind of justification. Post.3 is also the justification for the next circle, the one with center B and radius BA.
Now, the two circles meet, so let C be one of the points where they meet. You’ll notice that this is not justified, even though it’s obvious. But obvious isn’t enough. Sometimes statements seem obvious, but they’re actually wrong. It’s important in mathematics to know why you accept a statement, not just that you accept a statement. In this case Euclid should have included some postulate about when circles intersect.
The next construction is to draw straight lines CA and CB. These are justified by Post.1, which states that given two points, there is a line that has them as endpoints.
That concludes the construction part of the proof. The rest of it shows what has been constructed is an equilateral triangle. First, using the definition of a circle, Def.I.15 that all radii in a circle are equal, we conclude that line AC equals line AB, also that line BC equals line BA.
Next, we get to use a common notion as justification: C.N.1. For Euclid, a "common notion" was a statement about magnitudes in general that is to be assumed true. They are like postulates, but instead of being about geometry in particular, they’re about magnitudes. Logically postulates and common notions are both axioms--explicitly assumed statements. The magnitudes that appear in I.1 are the three straight lines AB, AC, and BC. Although Euclid does not explicitly state how, straight lines can be added, compared, and subtracted. All we need here is the case when straight lines are equal, and C.N.1. says
We now know that the three sides of the figure are equal straight lines. Therefore, we’ constructed an equilateral triangle on the given straight line AB, as required. The Guide below I.1 goes into further detail about critiques of the proof, but we will continue on with
Proposition I.2
To place a straight line equal to a given straight line with one end at a given point.
This second proposition, I.2 is also a construction. This time, the data include a point and a straight line (finite as usual), and the goal is to move the line over to the point; more precisely, to draw a line with one endpoint at the given point and equal to the given line.
This is the basic construction associated with a compass. You usually open the compass to a certain size, the length of a given line, and then draw a circle with a given center and that radius. But Euclid did not take this basic compass construction as a postulate because it is enough to assume a more limited postulate,
Post.3, the one we used in the first proposition. That corresponds to a compass that doesn’t transfer distances. Such a limited compass, which probably never actually existed, is called a "collapsible" compass.
The reason that a more limited postulate is enough is in the proof of this second proposition, I.2.
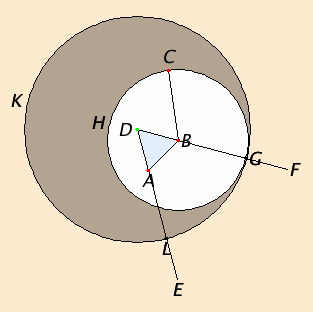
Note that the figure in I.2 varies quite a bit in its appearance depending on the relative positions and distances of the data.
As you study the construction, you’ll note that the construction we just made for an equilateral triangle is needed. Many of the propositions in the Elements, especially those in Book I, directly depend on the preceding proposition. Postulates 1 and three are used again, and for the first time Post.2, which allows a finite straight line to be extended indefinitely. Also I.Def.15, about equal radii in a circle, is used again, as is C.N.1.
C.N.3 is used for the first time:
The construction and the proof in this proposition take time to understand well enough to reproduce. Nonetheless, it’s rewarding to completely comprehend them, and valuable to understand that an ordinary compass can be simulated by a collapsible compass. Mathematicians often search for the simplest axioms and definitions for any field.
Proposition I.3
To cut off from the greater of two given unequal straight lines a straight line equal to the less.
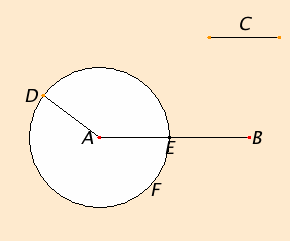The third proposition, I.3, is also a construction. It performs a subtraction of straight lines, that is, it is a construction to cut a smaller line off from a greater line. The construction is quite easy, given the previous construction in I.2, as is the proof that the construction works. Simply move the shorter line so that one of its endpoints coincides with an endpoint of the longer line, and draw a circle with that point as center and the moved shorter line as radius. That circle will cut off the correct length from the longer line.
No new definitions, postulates, or common notions are needed in the proof of I.3.
As mentioned in the guide to I.3, this proposition is used more than any other proposition in the Elements.