Proposition 44

To a given straight line in a given rectilinear angle, to apply a parallelogram equal to a given triangle.

Let AB be the given straight line, D the given rectilinear angle, and C the given triangle.

It is required to apply a parallelogram equal to the given triangle C to the given straight line AB in an angle equal to D.

I.44
I.42

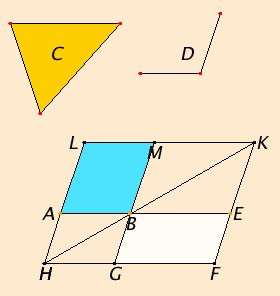
Construct the parallelogram BEFG equal to the triangle C in the angle EBG which equals D, and let it be placed so that BE is in a straight line with AB.

I.Post.2
I.31, I.Post.1

Draw FG through to H, and draw AH through A parallel to either BG or EF. Join HB.

I.29
I.Post.5

Since the straight line HF falls upon the parallels AH and EF, therefore the sum of the angles AHF and HFE equals two right angles. Therefore the sum of the angles BHG and GFE is less than two right angles. And straight lines produced indefinitely from angles less than two right angles meet, therefore HB and FE, when produced, will meet.

I.31

Let them be produced and meet at K. Draw KL through the point K parallel to either EA or FH. Produce HA and GB to the points L and M.

I.43

Then HLKF is a parallelogram, HK is its diameter, and AG and ME are parallelograms, and LB and BF are the so-called complements about HK. Therefore LB equals BF.

C.N.1

But BF equals the triangle C, therefore LB also equals C.

I.15, C.N.1

Since the angle GBE equals the angle ABM, while the angle GBE equals D, therefore the angle ABM also equals the angle D.

Therefore the parallelogram LB equal to the given triangle C has been applied to the given straight line AB, in the angle ABM which equals D.

Q.E.F.

Guide

 There are two steps in this construction. The first uses proposition I.42 to construct some parallelogram with the correct angle equal to the given triangle. The second uses I.43 to change its length to the proper length.

To “apply an area to a line in an angle” means just what this construction accomplishes, namely, to construct a parallelogram equal to that area with one side as the given line and one angle equal to the given angle.

In practice the angle is often a right angle. The given line may be thought of as a unit line. Then the length of the resulting rectangle represents the the area.

Use of Proposition 44

Besides being used in the next proposition, this construction is used in VI.25 to make a figure similar to one rectilinear figure but equal to another.